教师资格证考试过程中科目三数学笔试考察的内容相对比较难,线性代数部分往往是诸位考生觉得最为困难的备考部分,其主要原因是该部分内容为大学学习内容,在大学学习期间所学知识获得的练习比较少,在这里带领大家将考点进行相应的整理以供各位考试参阅。
接下来分析一下线性方程组考点及真题出题形式:
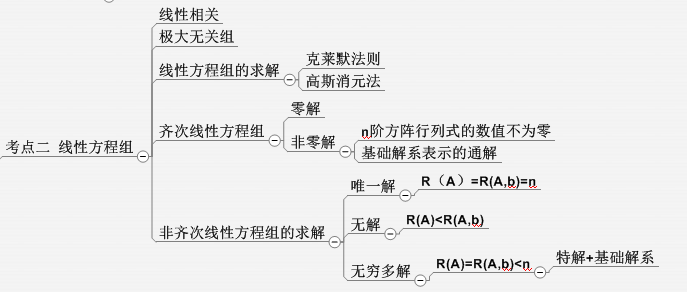
考生需要了解n维向量的概念,在了解概念的基础上能够利用初等变换计算向量组的秩和极大线性无关组,这部分是考试过程中的重点,因此一定要完全掌握。另外,齐次线性方程组解的结构和非齐次线性方程组解的结构也需要进行了解,知道其解的性质并能用特征向量进行表示。
【真题再现】

1.设是矩阵,其轶为3。考虑方程组。
![]()
(1)设为的两个解,为实数,证明也是的解;(4分)
![]()
(2)方程组的解空间的维数是多少?(无需证明)(3分)
【解析】
![]()
(1)因为,
![]()
所以齐次方程组的基础解系含有一个解向量。
![]()
故线性相关,则存在实数,使得
![]()
所以也是的解。
![]()
(2)齐次线性方程组解空间的维数
![]()
其中P是方程组的系数矩阵,是未知量的个数。
![]()
![]()
所以方程组的解空间的维数是1。
从这道题就可以看出矩阵初等变化和线性方程组解的结构,考察的内容非常基础。
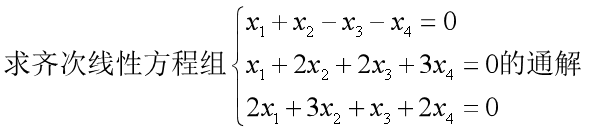
2.(2016年下半年,初中)

【解析】对系数矩阵进行初等变换得出R(A)=2,因此基础解析中含有4-2=2个解向量,通解的方程组为,
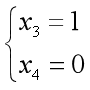
令,可得,令,可得
所以方程的基础解析表示为获取更多相关公考资料详情咨询白城华图——W13324369361









