逻辑运算的真假类型的题目,如果告知几句陈述中,只有一真(假),而能在几句陈述中找到一对矛盾命题,那么显然矛盾命题以外的命题就都是假(真) 的;如果告知几句陈述中,只有一真(假),而能在几句陈述中找到一对命题之间为下反对(反对)关系,那么显然真(假) 命题就在两个成下反对(反对) 关系的命题中,而下反对(反对)关系命题以外的命题就都是假(真) 的;如果告知几句陈述中,只有真(假),而能在几句陈述中找到一对命题之间有“A→B”的关系,那么就可知 A是假的(B是真的)。

　　性质命题分类表

量项	联项	命题类型	结构式	符号表示	简称	举例
全称	是	全称肯定命题	所有S都是P	SAP	A	所有 被 苍 蝇 叮 的鸡蛋都有缝
不是	全称否定命题	所有S都不是P	SEP	E	所有 的 黑 洞 都 不能反射光
特称	是	特称肯定命题	有的S是P	SIP	I	有些 中 国 人 会 说日语
不是	特称否定命题	有的S不是P	SOP	O	有些 汽 车 不 用 汽油作燃料
单称	是	单称肯定命题	这个S是P	爱因 斯 坦 出 生 在德国
不是	单称否定命题	这个S不是P	圆 明 园 不 在 苏州

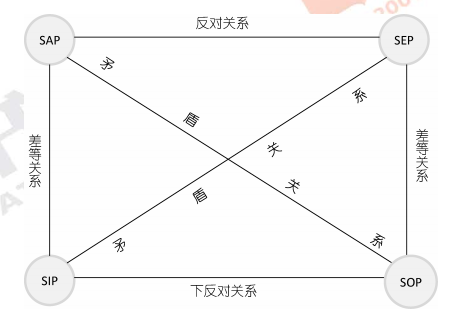
　　逻辑方阵(对当方阵)

　　运用对当关系的逻辑方阵进行的性质命题推理表

对当关系	特征	推理	无法推出
反对关系	不能 同 真,可 以同假	一个命题真,另一个 命题必假	一个 命 题 假,另 一 个 命 题真假不定
下反对关系	可以 同 真,不 能同假	一个命题假,另一个 命题必真	一个 命 题 真,另 一 个 命 题真假不定

对当关系	特征	推理	无法推出
矛盾关系	既 不 可 同 真,又 不 能 同假	一个命题真,另一个 命题必假; 一个命题假,另一个 命题必真
差等关系	既可 同 真,又 能同假	全称真,特称真; 特称假,全称假	全称假,特称真假不定; 特称真,全称真假不定

想要了解更多信息，请关注吉林华图公众号或者直接联系我们，电话号：19969533552（微信同步）