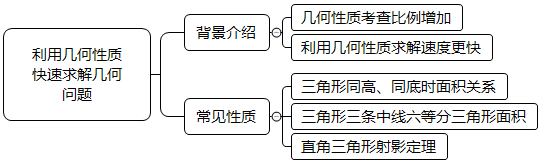
几何问题在行测考试中出现的频率非常高，难度适中，是比较好得分的一种题型。近几年不再纯粹的考察几何公式的计算，对几何性质的考察越来越多，所以对于常考的性质各位考生一定要熟悉，而且利用几何性质去求解几何问题可以大大提高解题的速度。下面就常考的几何性质进行梳理。

　　第一，两个三角形同高，则其面积之比等于底边之比;两个三角形同底，则其面积之比等于高之比。

　　【例1】如图所示，公园有一块四边形的草坪，由四块三角形的小草坪组成。已知四边形草坪的面积为480平方米，其中两个小三角形草坪的面积分别为70平方米和90平方米，则四块三角形小草坪中最大的一块面积为多少平方米?

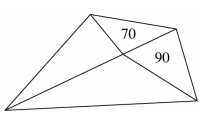
　　A.120B.150

　　C.180D.210

　　解析：给图形中的交点标上字母，同时过A点做底边的垂线为AE，过C点做底边的垂线CF。如下图所示：

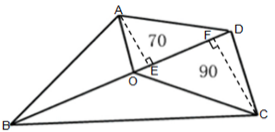
　　三角形AOD和三角形COD都可以把OD看做底边，两个三角形同比则面积之比就会等于高之比，因此AE：CF=70：90=7：9，而三角形AOB和三角形COB都可以把BO看做底边，因此，而，因此面积最大的三角形COB，。因此选A。

　　第二，三角形的三条中线会相交于一点，而且会把三角形分成面积相等的六个部分。

　　【例2】如图三角形中，A、B分别为两条边的中点，则图中阴影部分面积为三角形总面积的()。

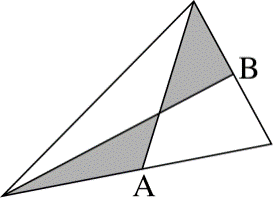
　　A.1/3B.1/4

　　C.2/7D.3/8

　　解析：画出第三边的中线，三条中线一定会相交于同一点，如下图所示：

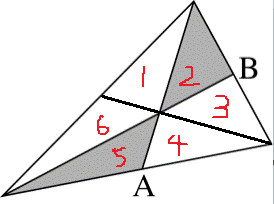
　　则整个三角形就分成了六个面积相等的部分，而阴影部分的面积就是其中的两个，因此图中阴影部分面积为三角形总面积的1/3。所以选A。

　　第三，射影定理，在直角三角形中，斜边的垂线的平方等于斜边上被垂线分开的两条线段的乘积。如图所示：BD2=AD×CD。

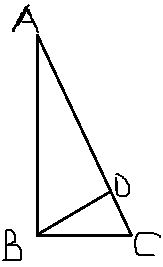
　　【例3】一块长方形土地ABCD中绘有3条会侧线如图所示。已知AE和CF垂直于对角线BD，AE、EF分别长8米和12米。问整块土地的面积为多少平方米?

　　A.96B.156

　　C.160D.240

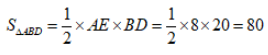
　　解析：设BE=x，则DE=12+x。AE垂直BD，所以AE2=BE×DE，即64=x(12+x)，解得x=4。则BD=20。，整块土地的面积为160，所以选C。

　　通过以上的例题，大家可以感受到，只要熟悉相关的几何性质，在面对一些几何问题时就可以快速的求解。几何性质还有很多，大家可以在刷题的过程中，对遇到的性质进行记忆。在考试中遇到了就可以直接拿来使用，加快做题的速度。

　　想要了解更多公务员考试技巧,添加抚松华图微信号19969533559