在图形推理中，空间重构类的题目中，有些题目会考察给定一个立体图形，选项当中哪一个是它的外表面?像这样的题目就是从选项当中找一个能够折叠成所给的立体图形这样的选项。这类题目主要考察空间想象能力，如果空间想象能力比较好的话不利用方法也可以做出来，但对于空间想象能力不好的同学就不太友好了，但是在做此类题目是有做题方法的，利用方法是能够解决的。

　　像这类题目的话不同的题目他们有不同的做题方法，常见的、常用的做题方法有：公共边等长法、公共点法和公共边法(公共边两个面是否对应)。

　　一、公共边等长

　　1、以下为给定的立体图形，下列那个选项可以折叠成该立体图形的外表面()

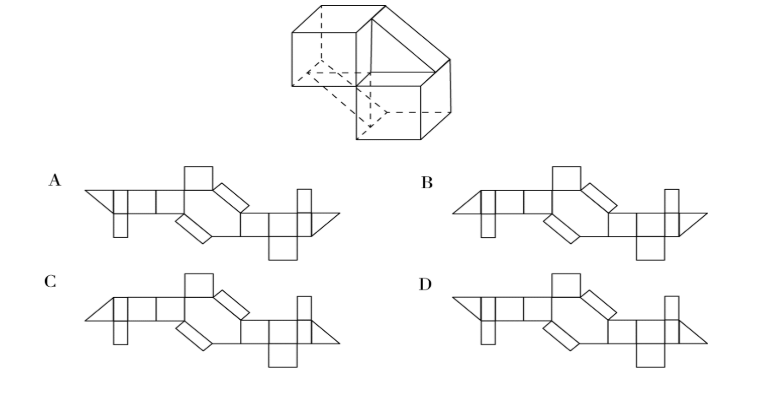
　　【答案】B

　　【解析】

　　第一步，本题考查不规则立体图形的空间重构。

　　第二步，分析选项。

　　四个选项的差异就在于两个等腰直角三角形和小长方形的相对位置。在已知图形中两个等腰三角形的两条直角边都和小长方形的长边重合。如图：

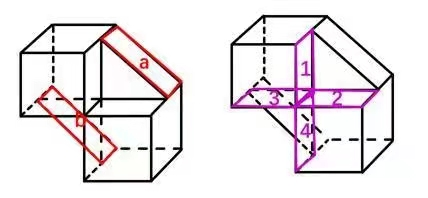
　　小长方形的长边和直角三角形的直角边是重合边(公共边)等长的关系，所以A选项左边等腰直角三角形，C选项右边等腰直角三角形，D选项两边等腰直角三角形都不符合，只有B项符合。

　　因此，选择B选项。

　　二、公共点法

　　2、下边是给定的立体图形，以下哪一项是该立体图形的外表面展开图?()

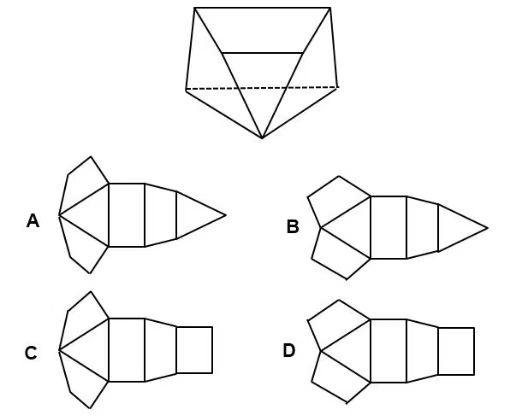
　　【答案】A

　　【解析】

　　第一步，本题考查不规则立体图形的空间重构。

　　第二步，分析选项。

　　题干立体图形中有两个三角形，而C、D项中都只有一个三角形，排除。第一种方法：对比A、B项发现，两者区别在于梯形的位置，根据题干可知两个梯形的长腰有公共点，A项中有公共点，而B项中这两条边不存在公共点，排除B项(公共点法)。第二种方法：利用相邻边的特性，题干立体图形左右两个梯形，与里面四边形面的公共边都是两个直角边，排除B选项(公共边等长法)。

　　因此，选择A选项。

　　公共边法(公共边两个面是否对应)

　　下图是给定的多面体，其可以由以下哪一图形为外表面折出?()

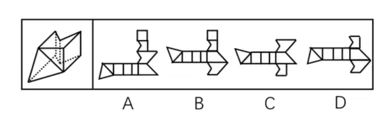
　　【答案】D

　　【解析】

　　第一步，本题考查不规则立体图形的空间重构。

　　第二步，分析选项。

　　给定的多面体由8个面组成，A、B项均是9个面，排除。关于C、D项，如下图：

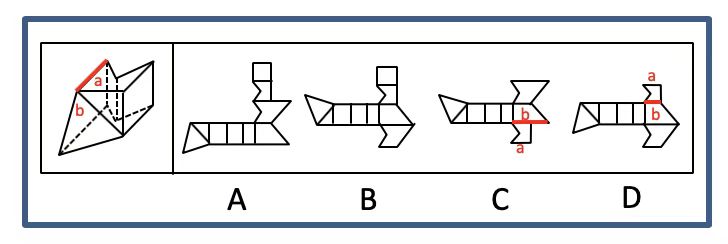
　　在多面体中，a面与b面(左侧的面)相连的线是b面里平行线中的短线，C项中是长线，排除，D项中是短线，符合。

　　故正确答案为D。

　　因此，选择D选项。

　　从上面三道题我们可以看出，像这类折纸盒、空间类“外表面折叠立体”的题目做题的时候是有方法有技巧的，空间想象能力不是很好的同学同样也可以做出来。大家做题的时候就先分析选项的不同点，根据他们的不同点判定该从哪个方向去分析，可以利用公共边等长、公共点等方法解决这类题目。