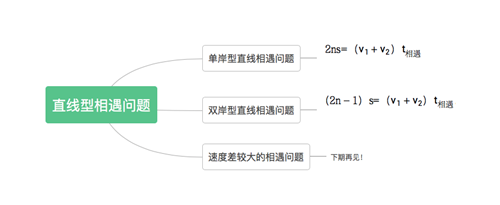
在近几年的省考当中,随着数量问题整体难度的上升,行程问题也向着更难迈出了步伐。在这样的情况下,直线型多次相遇问题的出现就变得频繁了起来。今天,华图教育就为大家带来直线型多次相遇问题的解题方法,让我们能用公式解决此类题目。
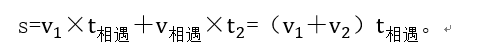
我们先来回顾以下我们之前所学的单次相遇问题。如图所示:对于单次相遇,我们可以理解为两人共同走完了这段路,即总路程为路程和。得到公式

还是同样的情景,当两人从A,B两岸相向而行开始,我们一直不停止的话就回得到下图:
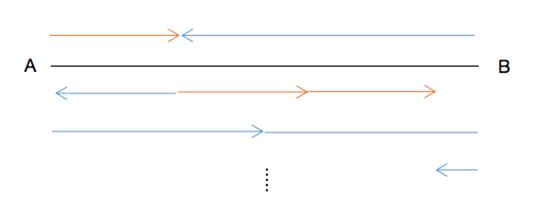
我们可以发现:第一次相遇是两人合作走完了一次这段路的话,从第一次相遇到第二次相遇,我们可以视为两人合作走完了两次这段路。而且,从第二次相遇到第三次相遇,也可视为两人合作走完了两次这段路。
![]()
若把相遇次数设为n,不考虑第一次相遇的情况,那可以得到相应公式:
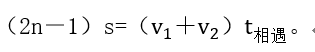
和之前的公式连立,我们即可得到双岸型相遇公式:
除此之外,还有一种模型:两人从同一点出发,对应得,我们称之为单岸型相遇模型。如图所示:
![]()
对于相遇进行讨论:可视为两人共同走完了两次全路程,若把相遇次数设为n,可用公式:
![]()
而之后再有相遇,则和双岸型后半部分相同,满足 两式并不冲突。
![]()
在同点出发的情况下,除同向出发之外,还可有异向出发,其路线图和第二次相遇之后的图示完全一致,即为:
![]()
故单岸型相遇公式为:
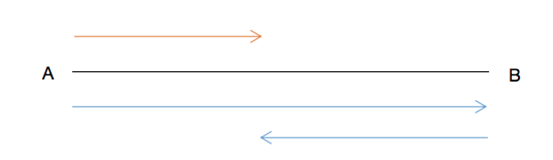
【例1】甲乙两人在相距120米的直路上来回跑步,他们同时从直路的两端出发,已知甲乙的速度比为7:5,则当两人第二次相遇时,甲走了多少米?
A.210
B.240
C.270
D.290
![]()
这道题,在我们学习了直线型多次相遇问题之后便得简单了起来。首先,通过读题我们可以判定这是一道双岸型的直线相遇问题,所用到的公式就是:
我们可以理解为:甲乙两人合作走完了3个120米,由于从运动开始到运动结束,甲乙两人均为停止运动,所以可以使用比例关系:在时间不变的情况下,速度与路程成正比,得到:由于甲乙两人速度之比为7:5,故甲乙两人路程之比也为7:5。
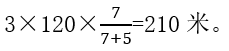
结合3个120米的信息,可以得到:甲走过的路程为
因此,答案选择A选项。
【例2】小张、小王二人同时从甲地出发,驾车匀速在甲乙两地之间往返行驶。小张的车速比小王快,两人出发后第一次和第二次相遇都在同一地点,那么小张的车速是小王的多少倍:
A.3
B.1.5
C.2
D.2.5
![]()
读题之后判断题型为单岸型的直线相遇问题,所用到公式:
题目的问题在询问小张和小王的速度之比。在题目中没有出现速度数据的情况下,一般考虑用比例关系解题。由于全程小张和小王都没有休息,故在时间一定的情况下,速度和路程成正比,故可将题目转化为对路程之比的求解。
对小王的路程进行分析,假设说小王第一次相遇行驶了x的距离,那么,当第二次相遇的时候,他又回到了第一次相遇的地点,结合其速度较慢,故其应该是从出发一段到达了另一段,又返回了相遇点,路程应为差一个x就正好跑完两次甲乙两地,故其路程可表示为(2s-x)。
从第一次相遇开始到第二次相遇,由于小王和小张的速度均为改变,而且路程和也为2s,故小王行走的路程依然为x。
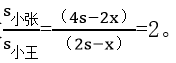
回顾整个过程,两人共同走完了4s,小王单人路程为2x,故小张单人路程为(4s-2x)。结合小王的路程为(2s-x),故
因此,答案选择C选项。
经过两道例题的讲解,相信大家对于直线型相遇问题已经有了自己的了解,在文章的最后,小编给大家留一个问题,假如在一百米跑道上,一位坐轮椅的老太太和刘翔从两端出发,相向而行做往返运动,那么请问,在第二次相遇的时候,他们两人的路程和是300米么?
留个小尾巴,我们下期再见!