行测中的数量关系模块题目难度较大,很多考生都为之头疼,其实我们只要掌握出题人考查的知识点,就能快速解题;下面给各位考生介绍一下几何问题如何快速解题,在几何问题的考查过程中,有一部分题目考查的是几何特性,只要我们掌握几何特性,题目就能迎刃而解。
一、几何的最值定理:平面图形中,若周长一定,越接近于圆,面积越大;若面积一定,越接近于圆,周长越小。立体图形中,若表面积一定,越接近于球,体积越大;若体积一定,越接近于球,表面积越小。
【例1】相同表面积的四面体、六面体、正十二面体及正二十面体,其中体积最大的是( )。
A.四面体 B.六面体
C.正十二面体 D.正二十面体
【答案】D
【解析】利用几何最值定理,题目中表面积相同的四种图形中,正二十面体最接近于球,故选D选项。
【例2】某健身馆准备将一块周长为100米的长方形区域划为瑜伽场地,将一块周长为160米的长方形区域划为游泳场馆。若瑜伽场地和游泳场馆均是满足周长条件下的最大面积,问两块场地面积之差为多少平方米?
A.625 B.845
C.975 D.1150
【答案】C
【解析】题目中周长一定,则越接近于圆,面积越大;瑜伽场地周长为100米,若要其接近于圆,则应为正方形,其边长为100/4=25米,面积为25×25=625平方米;游泳场馆周长为160米,若要其接近于圆,则应为正方形,其边长为160/4=40米,面积为40×40=1600平方米;故两场地面积之差为1600-625=975平方米,故选C选项。
![]()
二、几何的图形比例关系:若将一个图形尺度变为原来的N倍,则对应角度不变,对应周长变为原来的N倍,面积变为原来的倍,体积变为原来的N3倍。
【例3】某演播大厅的地面形状是边长为100米的正三角形,现要用边长为2米的正三角形砖铺满(如图所示)。问,需要用多少块砖?
A.2763 B.2500
C.2340 D.2300
【答案】B
![]()
【解析】利用几何图形比例关系,边长为2正三角形和边长为100的正三角形为相似图形,其边长比为2∶100=1∶50,则其面积比为1∶=1∶2500,故需要2500块砖,故选B选项。
【例4】如图,沙漏计时器由上下两个大小相同相互连通且底面互相平行的圆锥组成,下面的圆锥内装有细沙,计时开始时,将沙漏倒置,已知上面圆锥中细沙全部流下恰好需要1小时,则细沙高度下降一半所需的时间是:

A.30分钟 B.45分钟
C.47.5分钟 D.52.5分钟
【答案】D
【解析】利用几何图形比例关系,细沙高度下降一半,则剩余细沙的高和整个圆锥的高之比为1∶2,所以其体积之比为1∶8,则上半部分圆锥流出的沙子占整个圆锥的7/8,故其所需时间为60分钟×7/8=52.5分钟,故选D选项。
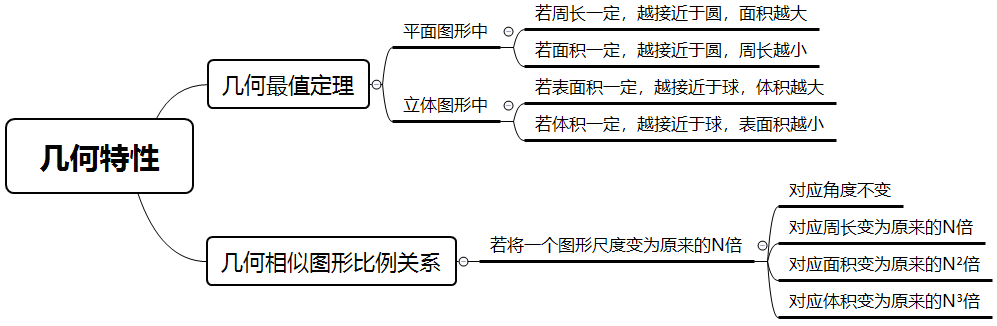
以上就是几何问题中运用几何特性快速解题的介绍,相信各位考生已经掌握了题目特征和用法,遇到类似题目能快速解题。下面通过思维导图总结今天的知识点,方便考生复习。









