数量关系是行测科目中最难的科目,也是众多同学准备“都选C”的科目。其实它没有想象中那么难,那么的无从下手,还是有许多小题型只要掌握公式、掌握规律就可以解决它。比如我们今天要给大家介绍的“天平称假币”问题。这种问题,如果是考场那种紧张的氛围下当场让你去思考,可能会稍有难度,但是提前要是有所研究,那基本就是秒杀题。今天我们就一起来研究一下:
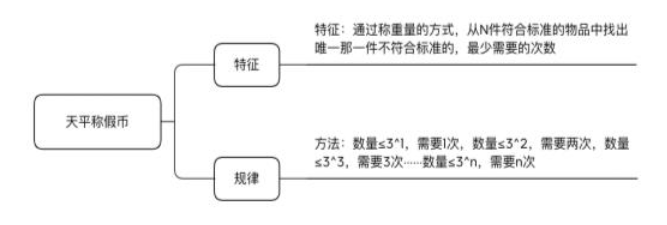
一、题型特点:天平称假币,假币除了重量是轻于真币,其他属性都相同。这个模型从表面去理解就是“从n枚硬币通过称重量的方式找出中找出唯一那枚假币,最少需要称几次?”,但是不是说所有题目都是让你去找假币的,假币可以认为是一件次品(除了重量不一样其他属性均相同)。总的来说这类题目就是:通过称重量的方式,从n件符合标准的物品中找出唯一那一件不符合标准的,最少需要的次数。
二、思维点拨
从2枚硬币中找出1枚假币,需要称1次,这大家都知道。那从3枚硬币中找出1枚假币,需要称几次呢?这里可能有不少同学说得称两次,其实也只需要一次,假设三枚硬币是A、B、C,先给A和B称一次,你会发现直接就能判断出来次品是哪个了,如果AB重量相等,那就说明那个假币就是C,如果AB重量不等,那轻的那个就是假币。那8枚假币呢?可以将硬币分成3堆:2枚、2枚、3枚,先称2枚和2枚,如果重量相等,那就是在3枚一堆,接下来只需要称一次即可;如果不等,那肯定就是在重量轻的那堆,无论是在哪个两堆,都只需要称一次即可,所以8枚硬币居然只需要称2次。

三、真题感知
【例】有24个外形完全相同的小零件,其中23个是正品,一个是次品,正品重量都相等,次品比正品稍重一些,用天平(无砝码)称,至少称( )次可以把次品找出来。
A.3
B.4
C.12
D.23
【答案】A
![]()
【解析】24个零件找1个次品,除重量外其他属性相同,本题就是一个运用“天平称假币”的模型。且,故只需要3次。
因此,选择A选项。
通过以上真题大家会发现,这类问题只要了解规律,考试一旦出现就是秒杀题,送分题。所以在备考过程中,大家不要畏惧数量关系,而是多去思考,多去总结,对于这种秒杀题一定要势在必得。真正的勇士是敢于直面数量关系,并且
战胜它,征服它。