环形相遇追及是行程问题的常考知识点,一般而言,环形相遇或追及的前提是同时同地出发,反向(或背向)而行是相遇过程,同向而行是追及过程。但近年的真题中,出现了甲乙两人从环形不同起点出发的情况,此时便不完全符合环形相遇或追及的模型,需要特别注意。
一、知识概览
甲、乙从环形不同起点出发,相向而行(如图1所示),一段时间后两人相遇,此次相遇虽在环形跑道发生,实际为直线相遇过程;相遇后两人位于环形同一起点,反向而行,为环形相遇过程,相遇一次共走一圈;相遇n次,路程和为nS。
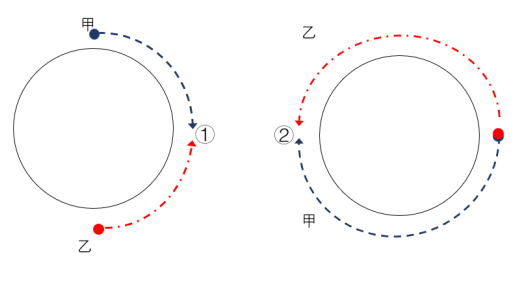
图1甲、乙从环形不同起点出发,相向而行
甲、乙从环形不同起点出发,同向而行(如图2所示),一段时间后快者第一次追上慢者,此次追及虽在环形跑道发生,实际为直线追及过程;追上后两人位于环形同一起点,同向而行,为环形追及过程,追上一次快者比慢者多走一圈;追上次n,路程差为nS。
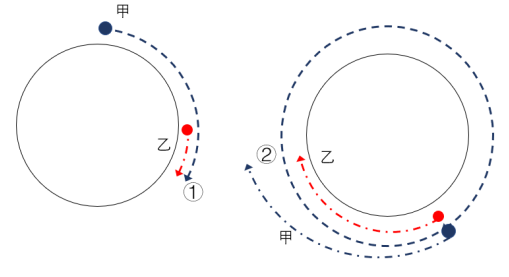
图2甲、乙从环形不同起点出发,同向而行
二、例题精析
【例1】甲、乙两名运动员在400米的环形跑道上练习跑步,甲出发1分钟后乙同向出发,乙出发2分钟后第一次追上甲,又过了8分钟,乙第二次追上甲,此时乙比甲多跑了250米,问两人出发地相隔多少米?
A. 200 B. 150
C. 100 D. 50
【点拨】甲、乙同向出发,为追及过程;乙出发时甲已跑步1分钟,在乙第一次追上甲前为直线追及过程,第一次追上后甲乙两人位于同一起点,环形追及开始,故第二次追上为环形追及。
【答案】B
【解析】第一步,本题考查行程问题,属于相遇追及类。
第二步,设两人相隔S米,则第一次追上,乙比甲多走S米。在400米的环形跑道上,从“第一次追上时”到“第二次追上时”,乙比甲多走400米。
第三步,“乙比甲一共多跑的250米”为第一次多跑的距离S与第二次多跑距离400米之和,即250=S+400,解得S=-150,即两者相隔150米。
因此,选择B选项。
拓展:-150米的负号表示方向,不影响两者之间的距离值。
【例2】王大妈与李大妈两人分别从小区外围环形道路上A、B两点出发相向而行。走了5分钟两人第一次相遇,接着走了4分钟后,李大妈经过A点继续前行,又过了26分钟两人第二次相遇。问李大妈沿小区外围道路走一圈需要几分钟?
A. 54 B. 59
C. 60 D. 63
【点拨】两人相向而行,为相遇过程;不同起点出发,第一次相遇为直线相遇,第一次相遇后两人位于同一起点,环形相遇开始,故第二次相遇为环形相遇。
【答案】A
【解析】第一步,本题考查行程问题的相遇问题,用相遇公式和比例法解题。
第二步,由第一次相遇时王大妈和李大妈所用时间均为5分钟,后期李大妈走王大妈一开始的路程所用时间为4分钟,根据行程公式可知路程一致,王、李两位大妈时间比为5∶4,则两人速度之比为4∶5。
第三步,两人从第一次相遇到第二次相遇所走路程为一个环形周长,那么李大妈单走一圈所用时间为(5+4)×(4+26)÷5=54(分钟)。
因此,选择A选项。
【小结】










