公考的小伙伴们应该都知道,在我们数量关系模块中有着这样一个考点——数列构造,数列构造问题是属于最值问题中的一个知识点,可能因为它的江湖地位没有行程问题、工程问题、经济利润问题那么高,难度也不能与排列组合、概率等相提并论,导致大家都忽略了这个简单的小可爱,今天呢,我们就一起来扒一扒数列构造这个小迷宫的面纱。
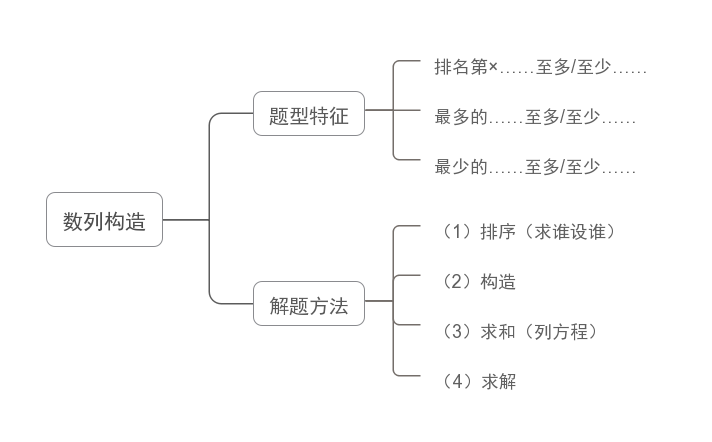
在认识数列构造之前,首先,我们要知道,我们应如何在万千题目中辨认出数列构造,也就是说我们要先去了解数列构造的题型特征是什么?如果题目的问题中出现了“排名第×……至多/至少……”、“最多的……至多/至少……”或“最少的……至多/至少……”,则这个题目就是数列构造问题。例如:①现有21本故事书要分给5个人阅读,如果每个人得到的数量均不相同,那么得到故事书数量第3多的人至少可以得到多少本?②现有21本故事书要分给5个人阅读,如果每个人得到的数量均不相同,那么得到故事书数量最多的人至少可以得到多少本?这些题目就是典型的数列构造问题,掌握了其题型特征及问法后,我们就可以根据数列构造的特定方法进行解题。
接下来,我们就一起来了解一下数列构造的四步解题方法:(1)排序(问谁设谁);(2)构造;(3)求和(列方程);(4)求解。
并通过下面的这道真题来进行说明。
【例】(2020年内蒙古)从某物流园区开出6辆货车,这6辆货车的平均装货量为62吨,已知每辆货车载重量各不相同且均为整数,最重的装载了71吨,最轻的装载了54吨。问这6辆货车中装货第三重的卡车至少装载了多少吨?
A.59B.60
C.61D.62
【答案】B
【解析】本题问“这6辆货车中装货第三重的卡车至少装载了多少吨”,符合数列构造的题型特征。我们使用数列构造的解题方法进行解答:
(1)排序,根据题意,按照载重量从重到轻依次给货车从1号到6号进行排序并编号,并将第三重的卡车设为x;
(2)构造,题目中要求“第三重的卡车至少”,要使3号的货车装的最少,其他的货车就要装的最多,又因为每辆货车载重量各不相同且均为整数,可列下表,
| 货车序号 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 |
| 载重量(吨) | 71 | 70 | x | x-1 | x-2 | 54 |
(3)求和,根据题意,可列方程:71+70+x+(x-1)+(x-2)+54=62×6;
(4)求解,解得x=60。
因此,选择B选项。
如果本题最后的问题变为“这6辆货车中装货第三重的卡车至多装载了多少吨”,则:
排序,排序方式不变;
(2)构造,要使第三重的卡车装的最多,其他的货车就要装的最少,又因为每辆货车载重量各不相同且均为整数,可列下表,
| 货车序号 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | ||
| 载重量(吨) | 71 | x+1 | x | 5 | 6 | 5 | 5 | 54 |
(3)求和,根据题意,可列方程:71+(x+1)+x+56+55+54=62×6;
(4)求解,解得x=67.5。
由于每辆货车载重量均为整数,因此,这6辆货车中装货第三重的卡车至多装载了67吨。
通过以上对数列构造的讲解和引入,希望能让大家对数列构造的题型特征和解题方法有一个简单的认识。