在百花齐放的行测数量规律里面，针对于面的考法可谓是花样繁多，五花八门，当然也是充满着“趣味”，今天我们就带大家一起来学习一下。首先，面的定义为白色的封闭区间，黑色的不算，不封闭的不算。把握着这个原则，当发现题干图形比较凌乱，窟窿多，面多的时候，我们就可以定位是要数面了。比如，下面这道题目：

　　【例题1】从所给的选项中，选择较合适的一个填入问号处，使之呈现的规律性：()。

　　【答案】A

　　【解析】步，观察特征。

　　组成元素不同，优先考虑数量类或属性类。每个图形均有封闭区间，考虑数面。

　　步，九宫格，横向规律无规律，考虑纵向规律。

　　列中，三个图形的面分别为2、4、2，列中的三个图形面的数量依次为4、3、1，前两列图形中面的总数均为8，第三列前两个图形的面的数量依次为5、1，所以问号处的图形面的数量应为2，只有A项符合。

　　因此，选择A选项。

　　这道题面多，定位到数面，只不过利用九宫格考到了竖列加法运算。而除此之外，真正不好想到的考点，五花八门的考法才渐渐拉开序幕。我们就一起看下面的题目：

　　【例题2】从所给四个选项中选出较合适的一个填入问号处，使之呈现规律性：()。

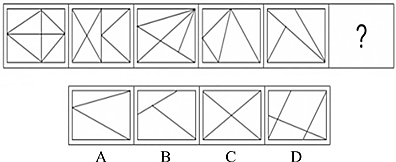
　　【答案】A

　　【解析】步，观察特征。

　　组成元素不同，优先考虑数量类或属性类。且每个图形均有封闭区间，考虑数面。

　　步，一条式，从左到右找规律。

　　题干图形面的数量依次为8、7、6、5、4、?，呈等差规律，问号处应选择面为3的图形，排除C、D项;题干图形面的形状均为三角形，只有A项符合。

　　因此，选择A选项。

　　以上这道题单看面的个数可以排除两个选项，还需要大家观察所有面的形状，才能选到正确的答案。这便是在数量的基础上，结合了对形状的考察。而这是观察所有的面，有时候也会针对部分相同形状的面进行考察，比如下面这道题：

　　【例题3】把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是:()。

　　A.①④⑤，②③⑥B.①⑤⑥，②③④

　　C.①③⑤，②④⑥D.①④⑥，②③⑤

　　【答案】B

　　【解析】步，观察特征。

　　图形组成不同，考虑数量类或属性类。图形出现相同形状的面，考虑数相同形状面的个数。

　　步，根据规律进行分组。

　　图形①⑤⑥相同形状面的个数均为4，图形②③④相同形状面的个数均为6，分为两组。

　　因此，选择B选项。

　　这道题就是考察部分形状相同的面，我们称之为相同面规律，除了像这样考察有几个相同面之外，还出现过考察相同面有几组等等。

　　【例题4】把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是：()。

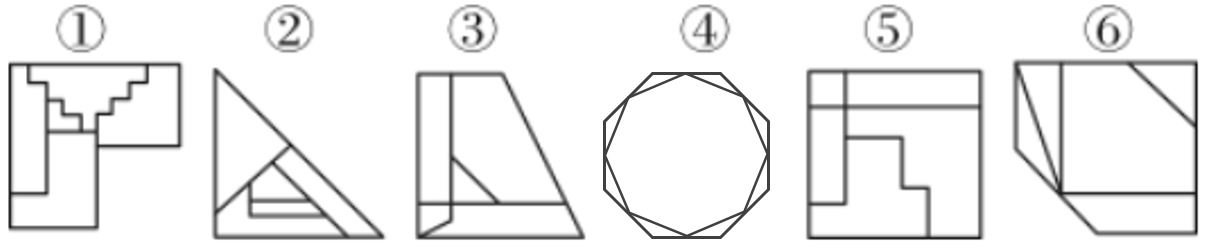
　　A.①③④，②⑤⑥B.①②⑥，③④⑤

　　C.①③⑤，②④⑥D.①④⑥，②③⑤

　　【答案】C

　　【解析】步，观察特征。

　　组成元素不同，优先考虑数量类或属性类。且每个图形均有封闭区间，考虑数面。

　　步，根据规律进行分组。

　　面的数量没有规律，考虑面的形状，图形①③⑤中较小面积面的形状与图形外边框一致，图形②④⑥中较大面积面的形状与图形外边框一致。

　　因此，选择C选项。。

　　较后便是对于某个面的考察，一般常考的就是较大面、较小面。可以单独考察较大面、较小面的形状，也可以考察较大面、较小面的属性，看是否是对称图形，对称类型是什么等等，以及像例题4的考法，考察较大面、较小面和外框的形状是否相同。

　　以上便是面的各种考法，虽然花样繁多，但只要同学们记住，面多就数面，简单数面选不到答案，那就看所有面的形状，还是不行就看是否有相同面，是否有较大、较小面，从他们入手。只要记住这些原则方法，那么五花八门的面规律也尽在我们掌握之中。