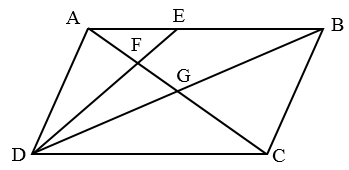
(单选题)平行四边形ABCD如图所示，E为AB上的一点，F、G分别是AC和DE、DB的交点。若AB=3AE，则四边形BEFG与ABCD的面积之比是：

　　A.2︰7

　　B.3︰13

　　C.4︰19

　　D.5︰24

　　正确答案：D

　　解析

　　第一步，本题考查几何问题，属于平面几何类，用赋值法解题。

　　第二步，题干没给出具体数值，可以采用赋值法解题。赋值AB=3，平行四边形ABCD的高为4，则AE=1;由于△AEF相似于△CDF，则两个三角形的高之比为AE：DC=1︰3，可知△AEF的高为4×=1。△ABG与△CDG全等，则△ABG的高为4÷2=2。

　　第三步，四边形BEFG面积=△ABG面积-△AEF面积=×3×2-×1×1=。四边形ABCD面积=3×4=12，两者之比为︰12=5︰24。

　　因此，选择D选项。