今天,就给大家讲解 数量关系中一种解法相对固定, 易掌握,好拿分的题型——数列构造。
一、题型特征
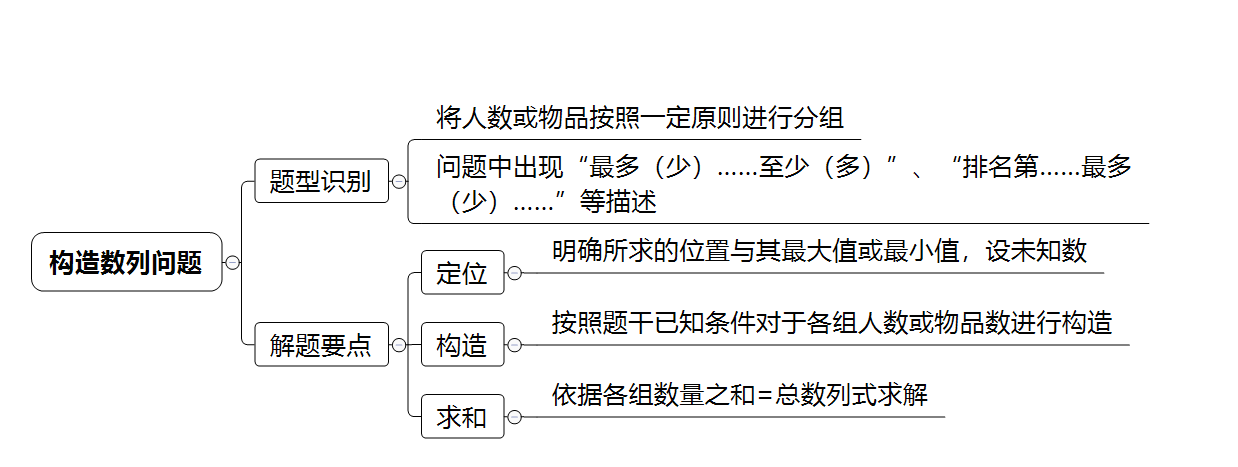
当题目中出现“最多(少)......最少(多)......”、“排名第......最多(少)......”这样的固定词组搭配时,能够确定它就是数列构造题。
【例】5个人钓了20条鱼,钓鱼数量最多的人最少可能钓了多少条?
【例】5个人钓了20条鱼,钓鱼数量第三多的人最多可能钓了多少条?
二、 解题要诀
定位—构造—求和
定位:将题目所要求的量设为x ,并明确x在所求对象中排的位次,求最多的人则x排在最大,求最小的人则 x 排在最小。
构造:将题目中所有出现的单位由大到小或由小到大依次排列开来, 并构造成一条数列。 当然 , 也要注意是否有可能出现各单位可以分配数量相等 的情况。
求和:将所有单位的量求和,列出方程并求解。需注意的是 有 可能所求出的解未必为整数解,那么只要遵循“问最小向上取整,问最大向下取整”的原则 即 可 。
三、 真题分享
【真题1】 现有21本故事书要分给5个人阅读,如果每个人得到的数量均不相同,那么得到故事书数量最多的人至少可以得到( )本。
A. 5
B. 7
C. 9
D. 11
【答案】 B
【解析】本题属于构造数列 问题 。要使得到最多的最少,那么其他人要尽可能的多,所以根据最多到最少依次可以构造出X、X-1、X-2、X-3、X-4,加和等于21,解得X=6.2,所以答案是7本。
因此, 本题 选择B选项。
【真题2】 有一座13.2万人口的城市,需要划分为11个投票区,任何一个区的人口不得超过其他区人口的10%,那么人口最少的地区可能有 ( ) 人?
A.9800
B .10500
C.10700
D .11000
【答案】D
【解析】第一步,本题考查最值问题,属于数列构造。
第二步,设最少的为x万人,那么最多的最多是1.1x。要使最少的最少,需 其他地区的人口最多,可构造11个投票区分别为10个1.1x和一个x。 第三步,根据总人数为13.2万,可得10×1.1x+x=13.2万,解得x=1.1。
因此, 本题 选择D选项。
通过上面两题的分享,相信大多数同学能够非常直观的感受到数列构造题目的出题特征 , 以及对应的解法。我们在解题的时候只需要牢牢把握住“定位—构造—求和”的固定套路,就能轻而易举地解决类似问题 。
试想一下,上一道题还是如同“天书”般的排列组合问题,令人百思不得其解,迷迷蒙蒙之中看到下一道题出现“最多(最少)”的字眼,是否会有柳暗花明又一村的惊喜呢?所以各位,数量切不可轻易言弃 ,2 022 省考,就让我们像构造数列一样,步步为营,列阵而行!