行测资料分析考试中,平均数考查频率很高。有些平均数的题目看似简单,但迷惑性很强,让不少考生处理起来不够顺畅。要么审题不清,不知道考什么;要么解题过程复杂,耗时较多。这类题目大多是平均数混合。今天,大家就跟着拨云见日,一起揭开平均数混合的面纱吧!
一、知识铺垫
1、题目涉及平均数,且存在部分概念与整体概念之间的加和关系,可考虑平均数混合;
2、混合平均数介于两个部分平均数之间,且更接近“份数”大的部分的平均数;通过两个部分平均数与混合平均数交叉作差,得到“份数”的比值。
二、经典例题
【例1】

问题:表中所列全国规模以上工业主要产品中,除生铁、粗钢、钢材和十种有色金属外,2020年8月产量超过1-7月月均产量的有多少种?
A.5 B.7 C.9 D.11

【答案】B。解析:“2020年8月产量超过1-7月月均产量”,即“2020年8月产量”。以此来比较表中7种产品的产量,计算量很大。整理不等式,可得“2020年8月产量×8>2020年1-8月产量”。这样比较虽然简单,但是很难记住结论,如果每次都去推导也会耗时。
仔细审题发现,“1-7月月均产量”是平均数,而“8月产量”也可看作8月这一个月的月均产量,此题考查平均数。从时间上看,8月、1-7月及1-8月存在部分概念与整体概念的加和关系。故考查平均数混合,即“8月产量”与“1-7月月均产量”混合得到“1-8月月均产量”。“8月产量超过1-7月月均产量”,由“混合平均数介于两个部分平均数之间”,可知8月产量>1-8月月均产量>1-7月月均产量。此题可转化为“8月产量超过1-8月月均产量的有多少种”。计算比较:
布:32>229÷8=2X,符合;硫酸:722>5385÷8=6XX,符合;
烧碱:319>2321÷8=2XX,符合;乙烯:179>1359÷8=16X,符合;
化学纤维:525>3827÷8=4XX,符合;水泥:22489>144229÷8=1XXXX,符合;
平板玻璃:8138>62309÷8=7XXX,符合;
符合条件的共有7种,选B。
小结:比较第N月与前(N-1)月平均数,考查平均数混合,可转化为比较第N月与前N月平均数。
【例2】
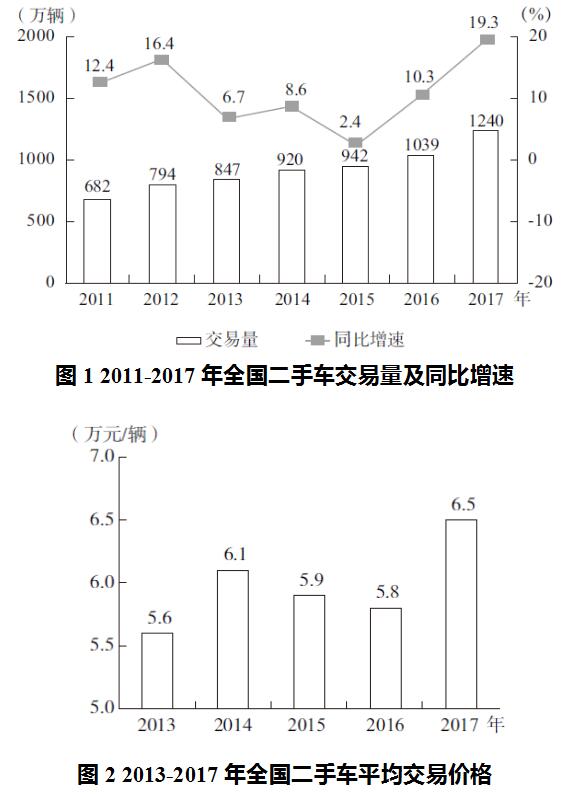
问题:2016-2017年,全国二手车平均交易价格在6.1万~6.15万元之间。(判断正误)

【答案】错误。解析:由材料可知,2016年、2017年全国二手车平均交易价格(平均数)分别为5.8万元/辆、6.5万元/辆,所求为2016-2017年平均交易价格,即2016年与2017年平均交易价格的混合。平均交易价格=,由“混合平均数介于两个部分平均数之间,且更接近‘份数’大的部分的平均数”,可知所求更接近于“交易量”(份数)大的2017年(1240万辆)的平均交易价格,即介于2017年平均交易价格与两年平均值之间,故<2016-2017年平均交易价格<6.5,所求在6.15~6.5万元之间,题干描述错误。
小结:此题容易看得出是平均数混合,但值得注意的是必须明确平均数的“份数”是哪个统计指标。
【例3】2018年,全国居民人均可支配收入28228元,同比增长8.7%。其中,城镇居民人均可支配收入39251元,同比增长7.8%;农村居民人均可支配收入14617元,同比增长8.8%。
问题:2018年,城镇居民与农村居民的人数之比约为:
A.11:9 B.9:11 C.3:2 D.2:3

【答案】A。解析:所求为人数之比,材料看似未给出人数的直接相关数据,不知从哪儿下手。但仔细分析不难发现,所求的人数即平均数“人均可支配收入”()的份数,又城镇居民、农村居民与全国居民存在部分概念与整体概念的加和关系,故考虑平均数混合。由“两个部分平均数与混合平均数交叉作差,得到‘份数’的比值”可得:

小结:此题难点在于判断考点,其关键是要看明确所求统计指标与材料统计指标之间的关系。
随着上述例题的解答,我们一起揭开了蒙在平均数混合问题上的那一层层面纱。









