在资料分析题目中，增长率计算属于大类题型，其中又存在着大量的计算增长率需考生计算增长率超过1%、10%、20%……，在这些题目中一般问超过的个数，少则五六个，多的会达到十个以上，很多考生如果没有技巧会导致费时费力且易错。

　　今天，我们就为大家详细介绍巧解这类题目的方法：错位相加。若一个题目问增长率超过10%的有几个，我们可以从增长率计算的公式出发：，要使得增长率>10%，可得>10%，化简可得，即，10%在计算的过程中给不会影响有效数字，只会影响数量级，小数点往左移一位错位相加就可以得到最后的结果，省时省力。我们以三个例题为例：

　　例1：2011—2018年间,我国海洋主题公园非门票收入同比增速超过10%的年份有几个?

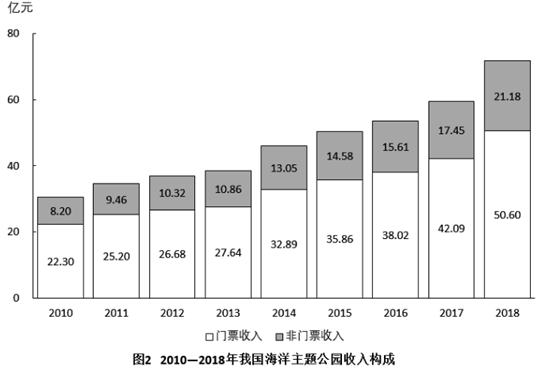
　　A. 3 B. 4

　　C. 5 D. 6

　　【解析】：第一步，本题考查增长率计算比较。

　　第二步，定位图2可知，2011~2018年间，我国海洋主题公园的非门票收入。

　　第三步，根据增长率=-1，若要使增长率>10%，则。2011年：9.46>8.2+0.82;2012年：10.32<9.46+0.946;2014年：13.05>10.86+1.086;2015年：14.58>13.05+1.305;2016年：15.61<14.58+1.458;2017年：17.45>15.61+1.561;2018年：21.18>17.45+1.745;故同比增速超过10%的有2011、2014、2015、2017、2018年这5个年份。

　　因此，选择C选项。

　　从例1我们可以看出，错位相加将乘法变成了简单的加法，高效又准确的解决了此类问题，我们再以两个例题巩固一下：

　　例2：(2017江苏)2006~2015年我国原煤产量年增长率超过10%的年份个数有：

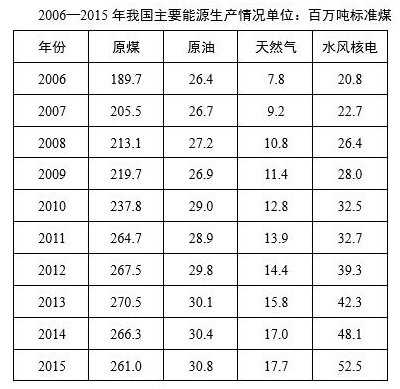
　　A. 0个 B. 1个

　　C. 2个 D. 3个

　　【解析】：第一步，本题考查增长率计算问题。

　　第二步，定位表格“原煤”所在列。

　　第三步，2014年和2015年原煤均为同比减少，排除。根据增长率=-1，若要使增长率>10%，则。2007年：205.5<189.7+18.97;2008年：213.1<205.5+20.55;2009年：219.7<213.1+21.31;2010年：237.8<219.7+21.97;2011年：264.7>237.8+23.78;2012年：267.5<264.7+26.47;2013年：270.5<267.5+26.75。故年增长率超过10%的只有1年，为2011年。

　　因此，选择B选项。

　　从以上两个例题可以看出，当题目中问增长率超过10%，错位相加能够简化计算，做到解题又快又准，那如果不是10%这种简单的小数点的移动呢?我们以例3为例，错位相加照样会比传统的方法简单。

　　例3：(2021国考)2014—2019年间，全国地铁运营线路长度同比增长20%以上的年份有几个?

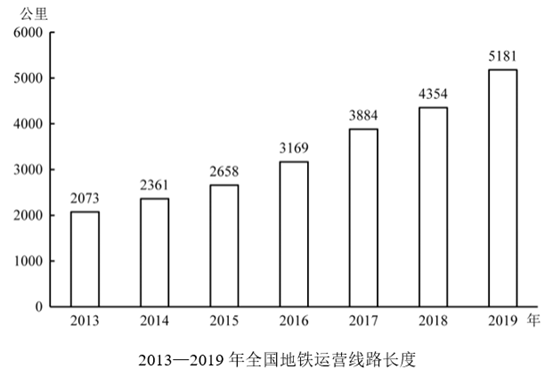
　　A. 1 B. 2

　　C. 3 D. 4

　　【解析】：第一步，本题考查增长率计算比较。

　　第二步，定位柱状图。

　　第三步，根据增长率=-1，若要使增长率>20%，则。代入数据可得，2014年：2361<2073+2073×20%=2487.6;2015年：2658<2361+2361×20%=2833.2;2016年：3169<2658+2658×20%=3189.6;2017年：3884>3169+3169×20%=3802.8;2018年：4354<3884+3884×20%=4660.8;2019年：5181<4354+4354×20%=5224.8，故同比增速超过20%的仅有2017年这1个年份。

　　因此，选择A选项。

　　从例3可以看出，现在的考题已经不仅仅局限于10%了，同学们要学会以不变应万变，熟练掌握错位相加的思想和方法，方能在考场上事半功倍，将分数牢牢掌握在自己手中。