在公考行测数量关系考试中，工程问题属于其中较为简单的一类题型，原因在于大部分工程问题都有一定的套路或者模版去解决问题，而很多考生所有的数量都不去做，这对于大家考试得高分或者上岸来讲，其实是不利的，今天我们就一起来深挖工程问题中的一个小版块——给定效率型，帮助大家在考试中拿下这类考题!

　　一、效率型的解题方法：赋值

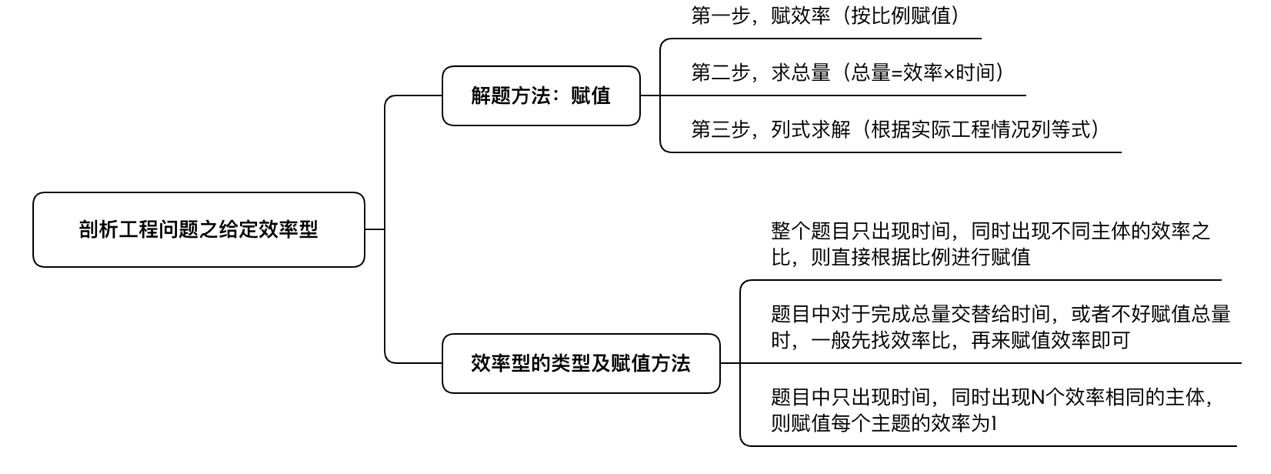
　　第一步，赋效率(按比例赋值)

　　第二步，求总量(总量=效率×时间)

　　第三步，列式求解(根据实际工程情况列等式)

　　二、效率型的类型及赋值方法

　　1.整个题目只出现时间，同时出现不同主体的效率之比，则直接根据比例进行赋值。如下面这个例题：

　　【例】甲、乙、丙三人共同完成一项工程，他们的工作效率之比是5∶4∶6。先由甲、乙两人合作6天，再由乙单独做9天，完成全部工程的60%。若剩下的工程由丙单独完成，则丙所需要的天数是：

　　A. 10

　　B. 12

　　C. 9

　　D. 15

　　【答案】A

　　【解析】第一步，本题考查工程问题，属于效率类。

　　第二步，由效率之比是5∶4∶6，赋值甲、乙、丙的效率分别为5、4、6。根据甲、乙两人合作6天，再由乙单独做9天，完成全部工程的60%，可得工程总量为。

　　第三步，剩下的工程量为150×40%=60，丙单独完成需要60÷6=10(天)。

　　因此，选择A选项。

　　2.题目中对于完成总量交替给时间，或者不好赋值总量时，一般先找效率比，再来赋值效率即可。如下面这个例题：

　　【例】某地计划修筑一条道路。如果该道路交由甲施工队先单独施工6天，乙施工队再单独施工15天即可完工;如果交由乙施工队先单独施工6天，那么甲施工队还需要单独施工24天才能修筑完成。如果这条道路交由甲施工队单独施工，道路修筑完成需要：

　　A.30天

　　B.32天

　　C.36天

　　D.40天

　　【答案】C

　　【解析】第一步，本题考查工程问题。

　　第二步，6甲+15乙=6乙+24甲，解得乙=2甲，那么赋值甲的效率为1，则乙的效率为2。这项工程的总量为1×6+2×15=36，甲施工队单独施工需要36÷1=36(天)。

　　因此，选择C选项。

　　3.题目中只出现时间，同时出现N个效率相同的主体，则赋值每个主题的效率为1。如下面这个例题：

　　【例】某工程50人进行施工。如果连续施工20天，每天工作10小时，正好按期完成。但施工过程中遭遇原料短缺，有5天时间无法施工，工期还剩8天时，工程队增派15人并加班施工。若工程队想按期完成，则平均每天需工作( )小时。

　　A. 12.5

　　B. 11

　　C. 13.5

　　D. 11.5

　　【答案】A

　　【解析】第一步，本题考查工程问题，用赋值法和方程法解题。

　　第二步，赋值每人每小时的工作效率为1，由题意得工程总量为50×20×10=10000。有5天时间无法施工，且剩8天时又增派15人加班施工，那么后8天有65人施工，前20-8-5=7(天)有50人施工。

　　第三步，设平均每天工作t小时，由总量不变可列方程：7×50×10+8×65×t=10000，解得t=12.5。

　　因此，选择A选项。

　　相信通过上面三个例题，各位小伙伴已经对工程问题中的效率型有了更深刻的理解，下次遇到这些特征的题目一定能拿下此类题，助力成“公”!

　　【思维导图】