对于逻辑判断这一模块，无论是国考、省考亦或者是事业单位考查均会有10道题，这10道题目所涉及的知识点也是较广的，有翻译推理、真假推理、分析推理、归纳推理、原因解析、加强论证、削弱论证等考点，每个考点也有自己的题目特征和解题方法。那今天就和大家谈谈逻辑难点之“真假推理”。

　　一、题型特征

　　“真假推理”这一考点的题目特征单独去说可能会很枯燥，那我们找两个例子一起去总结共性。

　　【例1】关于明天下雨情况，小明，小红和小丽三人有如下对话：

　　小明：明天的雨会下的像依萍找她爸爸要钱那天一样大。

　　小红：明天的雨不会下的像依萍找她爸爸要钱那天一样大。

　　小丽：明天会是大晴天。

　　三个人说的话中，只有一个是假的，那么，明天的天气情况是：

　　【例2】甲、乙、丙中只有一个会游泳，

　　甲说：“我会”

　　乙说：“我不会”

　　丙说：“甲说谎”

　　现知三人中只有一个人说的是真话。那么会游泳的是：

　　这两道例题考查的就是“真假推理”，观察发现：

　　第一个特点：例1中小明、小红、小丽三个人分别说了三句话，例2中甲、乙、丙三个人说了三句话;也就是几个人说了几句话，考查这几个命题之间的关系。

　　第二个特点：例1提问方式中提到“只有一个是假的”，例2提问方式中提到“只有一个人说的是真的”;也就是提问中有真假限定，涉及几真几假。

　　因此涉及上述两项特征的，即考查“真假推理”。那这一考点的解题思路呢?我们一起来看看吧!

　　二、解题思路

　　“真假推理”具体解题思路，如下图所示：

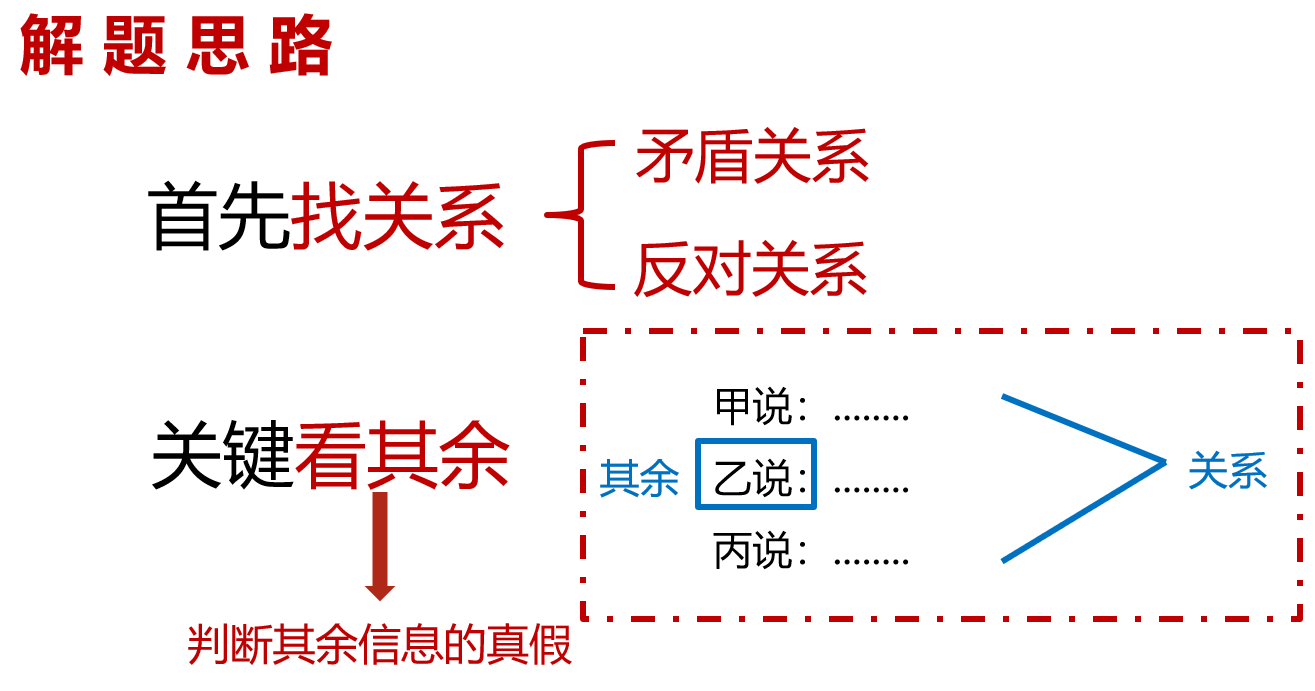
　　在这里，大家的疑惑点来了，第一步先找关系，找矛盾关系或者反对关系，那什么是矛盾关系、反对关系呢?这里就需要大家具体学习下面的相关知识点了。

　　三、知识点内容

　　(一)矛盾关系

　　矛盾关系的定义：是仅有两者存在的，非此即彼的关系。比如：男生和女生;开和关……

　　矛盾关系真假特性：必有一真，必有一假

　　因此，要想是矛盾关系，必须满足矛盾的真假特性。生活当中矛盾关系有很多，我们只需要掌握以下6组矛盾关系：

　　矛盾关系1：A是B 与 A不是B(可以直接记A与-A)

　　矛盾关系2：所有的S都是P 与 有的S不是P

　　矛盾关系3：所有的S都不是P 与 有的S是P

　　矛盾关系4：A →B 与 A 且 ¬ B

　　矛盾关系5：A且B 与 ¬ A 或 ¬ B

　　矛盾关系6： A或B 与 ¬A且¬B

　　例1：(2018年安徽)四位球迷在某球赛的晋级赛开始之前对几个队伍的赛况进行预测，他们比较关注其中的两支球队，分别作了如下预测：

　　方某说：如果甲队不能晋级，那么乙队也不能晋级。

　　白某说：不管甲队能不能晋级，乙队都不能晋级。

　　夏某说：乙队能晋级，但甲队不能晋级。

　　邓某说：我看这几支球队都不能晋级。

　　比赛结果证明，四位球迷中只有一位的预测是正确的。

　　根据上述情况，以下哪项一定为真?

　　A.白某预测是正确的

　　B.邓某预测是正确的

　　C.如果甲队能够晋级，那么方某的预测是正确的

　　D.如果甲队不能晋级，那么方某的预测是正确的

　　【答案】C

　　【解析】

　　通过题干中有若干论断以及只有一位预测正确，涉及几真几假，可以确定为真假推理。

　　按照真假推理题的解题思路，首先找关系。那就涉及对题干的整理，如下：

　　①¬甲→¬乙;

　　②¬乙;

　　③乙且¬甲;

　　④所有球队都不能晋级。

　　因此，其中①和③是矛盾关系(符合矛盾关系4：A →B 与 A 且 ¬ B)。

　　关键看其余。

　　根据矛盾关系的特性“必有一真，必有一假”及题干的真假限定“只有一位的预测是正确的”，则真话一定在①和③中，那么其余信息为假，即②白某的话和④邓某的话为假，排除 A 项、B 项。由②为假，可以推出：乙队晋级。C 项中，“甲队能够晋级”，根据“且关系”的特性“一假则假”，那么③为假，①就为真，即“方某的预测是正确的”，可以推出;D 项中，“如果甲队不能晋级”，结合“乙队晋级了”，根据“且关系”的特性“全真则真”，证明③为真话，那么①为假，即方某的预测是错误的，排除。

　　因此，选择 C 选项。

　　(二)反对关系

　　反对关系定义：除了已知的两方面之外还存在其他情况。

　　如右图，除了S和P之外，还有阴影这部分，即S和P是反对关系。

　　例如：白与黑;苦与甜

　　生活中的反对关系有很多，我们在学习过程中，只需要大家掌握以下这两组反对关系：

　　反对关系1：所有的S都是P 与 所有的S都不是P

　　例：所有的同学都是女生 vs 所有的同学都不是女生

	全女生	全男生	有男生有女生
所有的同学都是女生	真	假	假
所有的同学都不是女生	假	真	假

　　通过这两个命题在所有情况下的真假性发现，每一种情况下必有一假，甚至还存在两个都为假的。因此，可以简记：两个“所有”，必有一假，可以同假。

　　反对关系2： 有的S是P 与 有的S不是P

　　例：班里有的同学是女生 vs 班里有的同学不是女生

	全女生	全男生	有男生有女生
班里有的同学是女生	真	假	真
班里有的同学不是女生	假	真	真

　　通过这两个命题在所有情况下的真假性发现，每一种情况下必有一真，甚至还存在两个都为真的。因此，可以简记：两个“有的”，必有一真，可以同真。

　　例2：国家统计局到某单位开展反腐倡廉公众满意度调查，该单位包括局长在内共有 373名员工。有关这 373 名员工，以下三个断定中只有一个是真的：(1)有人满意;(2)有人不满意;(3)局长不满意。

　　根据这段文字，以下为真的是：

　　A.373 名员工都满意

　　B.373 名员工都不满意

　　C.有 1 名员工不满意

　　D.无法确定该单位满意人数

　　【答案】A

　　【解析】

　　题干存在若干论断及“只有一个是真的”有真假限定，确定为真假推理。

　　首先找矛盾：(1)有人满意和(2)有人不满意是反对关系。

　　关键看其余。

　　根据三个断定中只有一个是真的，再结合反对关系特性“必有一真”，可知(3)局长不满意为假，即局长是满意的。由局长满意可以推出有人满意，因此(1)为真。因为三个断定中只有一个是真的，所以(2)有人不满意为假，因此(2)的矛盾命题所有人都满意为真。

　　因此，选择 A 选项。

　　以上就是“真假推理”具体解题思路和相关知识点。“真假推理”是公务员考试中也会考查到的一种题型，它的方法性、技巧性很强。没学过相关技巧，会比较费时间，但是只要掌握了本文讲的方法，那么真假推理就是送分。