环形排列组合。
![]()
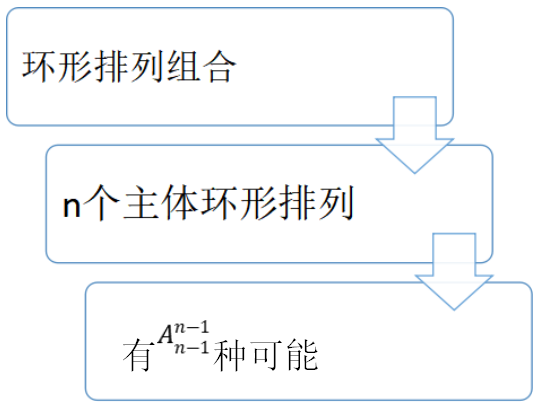
首先我们先来了解,什么是环形排列组合。环形排列组合的基本模型就是:“n个人围成一个圆圈,问:共有多少种不同的方法?”,公式:
【例1】有三个小朋友围成一圈做游戏,有多少种不同的排列方式?
A.6 B.4
C.2 D.1
【答案】C
【解析】第一步,识别题型,有n个人围成一圈,求多少种排列方式,考查环形排列组合;
![]()
第二步,套用公式,有=2种,故选C。
![]()
我们需要注意,这和之前遇到的站成一排进行排列是不一样的,所以排列的结果并不是。围成一圈,我们看的是所有人的相对顺序,举个例子,假如这三个人分别是甲、乙、丙。就甲而言,乙坐在他的左边丙坐在他的右边,和丙坐在他的左边乙坐在他的右边,这是两种完全不同的情况,并且总共也就只有这两种排列情况,如下图。

除此之外,不管我们以乙或者丙作为研究对象,或者是顺时针逆时针换位置,都会重复的情况。所以可以理解为,无论以谁作为研究对象都可以,先固定其中一人(是谁都一样),剩下的人进行全排列,所以三个人进行环形排列,总共有=2种不同的排列方式。因此如果是n 个人围成一圈,不同的排列方式有种。
【例2】有9个小朋友手拉着手围成一个圆圈做游戏,问总共有多少种不同的方式?
A.35280B.40320
C.362880D.456720
【答案】B
【解析】第一步,识别题型,有n个人围成一圈,求多少种排列方式,考查环形排列组合;
![]()
第二步,套用公式,有=40320种,故选B。
因此,选择B选项。
【例3】6个小朋友围成一圈做游戏,小华和小明需要挨在一起,问有多少种安排方法?
A.360B.240
C.120D.48
【答案】D
【解析】第一步,本题考查排列组合问题,属于方法技巧类。
![]()
第二步,将小华和小明绑在一起,相当于5个元素环形排列,小华和小明有顺序,则安排方法有X2=48(种)。
因此,选择D选项。
通过上面三道题目的讲解,相信同学们对于环形排列有了基本的认识与了解,我们会发现,只要能够识别题型,套用公式这类题型也并不难。但是在实际考试的过程中,为了增加题目的难度,很多题目会同例3一样,与排列组合中的其他方法相结合以考察考生的综合能力,在遇到此类题目的时候大家也不要有畏难心理,只需要按照每类题型所对应的解题方法做题即可。
思维导图
了解更多热点知识备考,请关注大安华图教育。微信:19990599397;咨询电话:0436-5348686









