方程是指含有未知数的等式。在数量关系中，解方程容易，但如何设未知数，正确的列出等量关系是一个难点，下面我们结合具体的题目分别讲解。

　　1.设所求量

　　例：(2020重庆)某企业员工组织周末自驾游，集合后发现。如果每辆小车坐5人，则空出4个座位;如果每辆小车少坐1人，则有8人没坐上车，那么，参加自驾游的小车有：

　　A.9辆B.10辆 C.11辆 D.12辆

　　解析：拿到一个题目，我们优先选择设所求量，简单粗暴，求谁设谁，可以直接设有X辆小车，通过两种安排员工的坐车方式的总人数相等，找出等量关系，在本题中出现的“如果…如果…”是一种天然的等量关系;

　　第一种坐车方式求员工人数：5X-4;第二种坐车方式求员工人数：4X+8;

　　5X-4=4X+8，解得X=12，选择D项;

　　本题小结：简单直接，优先设所求量。

　　2.设比例份数

　　例：(2018广西)年终某大型企业的甲、乙、丙三个部门评选优秀员工，已知甲、乙部门优秀员工数分别占三个部门总优秀员工数的1/3和2/5，且甲部门优秀员工数比丙部门的多12人，问三个部门共评选出优秀员工多少人?

　　A.120人B.150人 C.160人 D.180人

　　解析：在本题中，直接设优秀员工的总人数进行列式，不方便计算，因此我们考虑在设未知数时，通过题干中的信息，巧妙设置未知数，通过审题“甲、乙部门优秀员工数分别占三个部门总优秀员工数的1/3和2/5”我们可以得知，优秀员工的总人数应是3的倍数以及5的倍数，因此考虑设优秀员工人数为3和5的最小公倍数即15X人，则甲部门优秀员工数为15X×1/3=5X人，乙部门优秀员工数为15X×2/5=6X人，则丙部门优秀员工数=优秀员工的总人数-甲部门优秀员工数-乙部门优秀员工数=15X-5X-6X=4X人;再根据已知条件甲部门优秀员工数比丙部门的多12人找到等量关系，列出方程5X-4X=12，解得X=12人;则三个部门共评选出优秀员工人数为15×12=180人。

　　本题小结：题干中出现明显的比例关系时，考虑设比例份数。

　　3.设中间量

　　例：(2019江苏)某机关事务处集中采购了一批打印纸，分发给各职能部门。如果按每个部门9包分发，则多6包;如果按每个部门11包分发，则有1个部门只能分到1包。这批打印纸的数量是：

　　A.87包B.78包 C.69包 D.67包

　　解析：审题后发现，直接设打印纸的数量，不方便计算，但观察可知，打印纸的数量和部门的数量有关，因此考虑设出部门的数量，即可表示出打印纸的数量，设部门数量为X，按照之前总结的天然等量关系“如果…如果…”，按照第一种分发方式表示出打印纸的数量：9X+6;按照第二种分发方式表示出打印纸的数量：11X-10;列出方程：9X+6=11X-10，解得X=8，故打印纸的数量为9×8+6=78包，选择B项。

　　本题小结：当题干中的某个中间量与其他未知量存在联系时，设中间量可以方便列式。

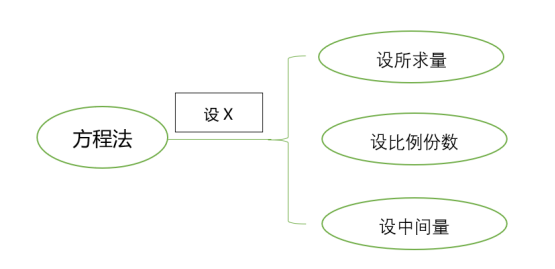
　　思路总结：

　　了解更多热点知识备考，请关注大安华图教育。微信：19990599397;咨询电话：0436-5348686