数量关系模块是历届考生反映最难的模块。在备考过程中，甚至有很多考生直接放弃数量关系模块。考生们认为数量关系知识点多，要求思维能力比较强，短时间以内很难提高得分能力。其实不然，通过短时间备考，在考试中拿一个不错的分数很简单。因为在实际考试中有一些题型套路比较固化，只需要学好套路即可。

　　今天我们学习一种套路题——效率制约型工程问题。该题型主要涉及三个量，工作总量、工作效率、工作时间。核心公式为：总量=效率×时间;解题方法主要有：方程法、赋值法、比例法。

　　效率制约型：在题干中直接给出各个主体之间效率的比例关系，常用数学表达式或文字阐述的形式呈现。

　　解题方法：赋值法。

　　解题步骤：

　　第一步，赋值效率。根据题干中的效率关系直接对各个主体的效率进行赋值。

　　第二步，求出总量或者时间。大多数情况下找时间求总量即可。

　　第三步，找等量关系解答。依据题意列出等式，进行解题。

　　例题分析：

　　【例1】某单位甲、乙、丙三人负责整理一项档案，他们工作5天完成了1/4，之后甲和乙因其他工作被调离，两天后才返回，期间丙继续整理档案。已知甲、乙、丙三人的工作效率之比为4∶3∶2，则完成这项工作共需要花费()天。

　　A.20B.21

　　C.22D.23

　　【答案】C

　　【解析】第一步，本题考查工程问题，用赋值法解题。

　　第二步，赋值甲的效率为4，乙的效率为3，丙的效率为2。三人合作完成全部工作需要20天。其中两天的工作量为(4+3+2)×2=18，但实际甲乙不在只有丙做，完成2×2=4，剩余18-4=14，还需要14÷(4+3+2)=，即2天。那么一共用20+2=22(天)。

　　因此，选择C选项。

　　【例2】有甲、乙、丙三个工作组，已知乙组2天的工作量与甲、丙共同工作1天的工作量相同。A工程如由甲、乙组共同工作3天，再由乙、丙组共同工作7天，正好完成。如果三组共同完成，需要整7天。B工程如丙组单独完成正好需要10天，问如由甲、乙组共同完成，需要多少天?

　　A.不到6天B.6天多

　　C.7天多D.超过8天

　　【答案】C

　　【解析】第一步，本题考查工程问题，属于效率类，用赋值法解题。

　　第二步，设三者工作效率分别为甲、乙、丙，根据题意则有：2乙=甲+丙，3甲+3乙+7乙+7丙=7甲+7乙+7丙→3乙=4甲，赋值甲=3，则乙=4，解得丙=5。

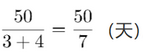
　　第三步，B工程总量=10丙=10×5=50，即甲乙合作需要，即7天多。

　　因此，选择C选项。

　　小结：工程问题中制约型题型属于该问题较难的题型，主要的难点是题干可能会通过文字的形式隐藏效率的比例关系。不管该提醒怎么变化，解题步骤永远为三步：赋值效率、找总量、求时间。