三集合容斥原理是公务员行测考试数量关系中常考的一个知识点,透彻地理解该知识点涉及的公式、计算方法是很必要的,同时掌握相应的技巧也可以帮助考生在有效的时间内高效准确地解题,为此山西华图就以上知识点的具体内容及解题技巧展开一个细致的讲解,我们先从基础知识开始。
在三集合容斥原理中,容斥原理的本质其实就是集合,而集合是指将同一属性的所有元素放在一起,当三个集合有交叉和融合时就是本节内容所提到的三集容合斥原理的问题,这个考点涉及的公式一般有三种,虽然公式很长,但是只要理解公式的含义,考试的时候更多的是机械代公式就可以了,这也是多省考试中一个比较稳定和主流的考法。常用的3个公式如下:
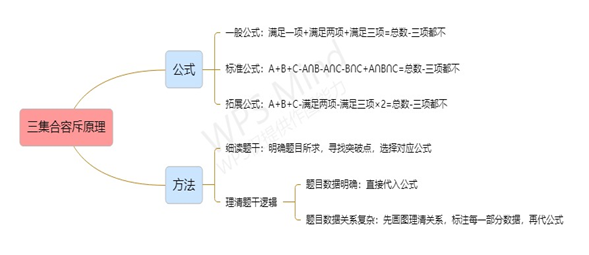
1.一般公式:满足一项+满足两项+满足三项=总数-三项都不
2.标准公式:A+B+C-A∩B-A∩C-B∩C+A∩B∩C=总数-三项都不
3.拓展公式:A+B+C-满足两项-满足三项×2=总数-三项都不
对于这三个公式,在考试时是可以直接套用的,但是若题中所给条件不明晰,不方便直接代公式时,建议大家可以优先考虑用画图法理清题目思路,再代公式计算。
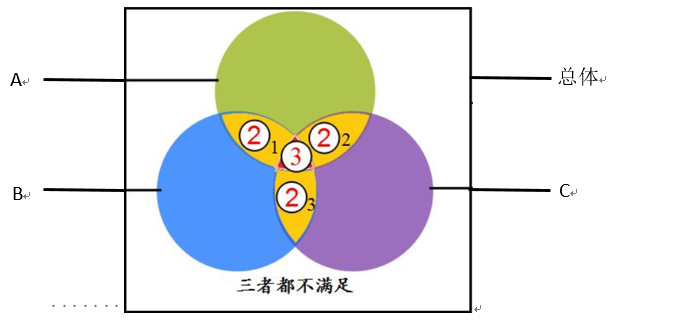
如上图,用一般公式:绿色部分加蓝色部分加紫色部分为满足一项,黄色标②的部分为满足两项,红色标③的部分为满足三项,按照一般公式的计算方法,有:(绿+蓝+紫)+②+③=总体-三者都不满足,若题目中给到相应数据,可直接代入求解。
用标准公式:A代表上面的圆圈,B表示左边的圆圈,C代表右边的圆圈;A∩B表示黄色的第一个区域和③合起来的部分,A∩C表示黄色的第二个区域和③合起来的部分,B∩C表示黄色的第三个区域和③合起来的部分;A∩B∩C表示③,我们发现A∩B、A∩C、B∩C中均有A∩B∩C表示的③这个部分,计算A+B+C的时候③被加了3次,同样在减A∩B、A∩C、B∩C的时候③也被减去了3次,所以在计算最后得再加一次③,这样才能把所有部分都加进去,故代入公式有:A+B+C-(黄1+③)-(黄2+③)-(黄3+③)+③=总体-三项都不,同样,当题目中有对应部分数字时可直接代入计算。
用拓展公式:A+B+C-满足两项-满足三项×2=A+B+C-黄1-黄2-黄3-2×③=总数-三项都不,因为A+B+C时把③加了3次,在减去黄1、黄2、黄3部分时并未减③,所以计算最后再减去两个③即可,其实拓展公式是标准公式的进一步计算,为了方便考生在考场上能根据题目已知条件直接运用所以把公式列出来。
以下通过几个例子来进一步巩固该知识点:
【例1】某单位举行篮球、长跑和跳绳比赛,规定每人最多只能报两个比赛,结果一共有40人报名,篮球、长跑和跳绳的报名人数分别为23人、15人、25人,且同时报篮球、长跑的有7人,同时报篮球、跳绳的有8人,那么同时报长跑和跳绳的人数为:
A.6 B.7
C.8 D.9
【答案】C
【解析】因为题目规定每个人最多只能报两个比赛,所以此题没有三种都报的人,我们设报篮球的为A,报长跑的为B,报跳绳的为C,那么A∩B∩C为0,A∩B=7,A∩C=8,所求为B∩C,根据标准公式:A+B+C-A∩B-A∩C-B∩C+A∩B∩C=总体-三项都不,总体为40,代入数据有:23+15+25-7-8-B∩C=40-0,得到B∩C=8,故选择C。
【例2】某校组织各科目模考比赛,且不限制报考科目数量,结果统计参加模考的人数为46人,其中参加语文模考的有26人,参加数学模考的人有25人,参加英语模考的有23人,且已知只参加了两门模考的人数为24人,问三门模考都参加的有几人?
A.6 B.2
C.3 D.4
【答案】B
【解析】参加语文的用A表示,参加数学的用B表示,参加英语的用C表示,只参加两门模考即为拓展公式中“满足两项”的,所求为“满足三项”的,因为题目中统计的就是参加模考的人,所以46人中每个人都是至少参加一项,“都不”=0,根据拓展公式:A+B+C-满足两项-满足三项×2=总数-三项都不,代入数据即:26+25+23-24-满足三项×2=46-0,得满足三项=2,故选择B。
【例3】某公司奖励员工去公费度假,暂定A、B、C三个景区,每位员工均可三个景区全部报名,员工可根据自己实际情况自行决定。报名结束后统计,共有76人报名,其中报名A、B、C景区的分别有34、23、30人,三个景区都报名了的有3人,求仅报了一个景区的有几人?
A.70 B.68
C.69 D.66
【答案】B
【解析】题目中统计的是报名人数,故此题中“都不”的人数为0,现知A+B+C=34+23+30=87,“满足三项”=3,根据拓展公式:A+B+C-满足两项-满足三项×2=总数-三项都不,代入数据,87-满足两项-3×2=76,得“满足两项”=5,再根据一般公式满足一项+满足两项+满足三项=总数-三项都不,有:满足一项+5+3=76,满足一项=68,故选B。
上述三个例题就是根据三集合容斥原理三个公式设定的,相信各位考生通过以上内容的学习可以对“三集合容斥原理”的考察内容、形式以及公式的运用有一个清晰的认知,最后希望大家可以通过练习大量习题来对本节所学内容进行巩固,熟练掌握。









