数量关系对于全国大多数考生而言,都是没时间做的,即使有时间也不一定做得出来。难道数量关系就这么放弃了吗?其实不然,你放弃数量关系,言语,判断,常识,资料分析能有个不错的正确率,总的来说行测的分数也是很乐观的。但是如果你想更上一层楼的话,数量关系不能放弃,得选择几个你擅长的题目做,剩下的再蒙一个选项,这样数量关系也能对一半以上,当然你数学底子好的话,就另当别论,全部拿下。
国考省考中数量关系的难度大多都在初中小学的奥赛难度,也有个别高中难度的题目。我们需要做的就是“知己知彼”,何为“知己知彼”?就是把简单点的常考的题目识别出来,拿下它们。剩下的题目看自身情况,没时间了就全蒙一个选项,这样正确率会高点。时间充裕的同学们全做完。接下来就是跟同学们介绍一下数量关系模块中的几何问题。
几何问题是考试中非常常见的一个题型,几乎年年必考。但是难度不一,整体而言难度在中上等。几何问题最大的特点就是杂,在备考时因为题型很多,解法也很多,所以同学们都举步维艰。下面给同学们介绍一个关于平面几个问题的解题小技巧。
测量法。使用范围:平面几何求长度、长度比、面积、面积比。因为在国考省考中,图形尺寸都很标准,只要能用上尺子测量,测出来的数据必然能给我们解题带来便利,有时候能直接选到答案。比如以下题目:
如下图所示,在直角三角形ABC中,MN是中位线。已知四边形ABMN与三角形MNC的周长比为28:15,则AC与BC的长度比是:
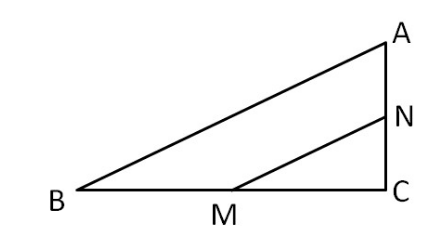
A. 5∶12
B. 5∶7
C. 3∶4
D. 6∶7
不难看出,这个题如果按照常规思路走需要花费一定时间,如果我们手上有一把尺子量出AC跟BC的长度,然后估出他们的比值,根据选项中的比值是不是直接就能选答案了?天下武功唯快不破,时间就是生命,时间就是分数,这个题就能直接拿下!
如下图,ABCD是一个梯形,E是 AD的中点,直线CE把梯形分成甲、乙两部分,其面积之比为5∶2,那么上底 AB 与下底CD的长度之比是:
A.2 :5
B.3 :5
C.3 :4
D.4 :7
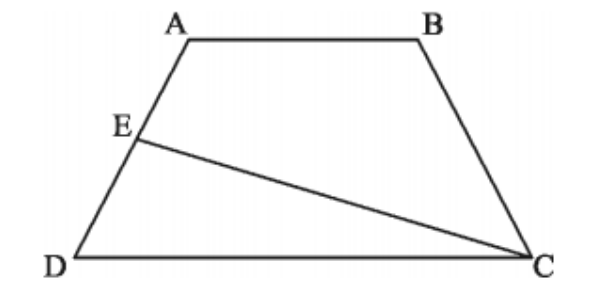
同样的这个题求长度比,我们是不是可以直接用尺子量出上底与下底的长度,然后根据所量的长度,结合选项估出一个比值,这样就能事半功倍了。
综上所述:如果我们在考试中遇到了平面几何类的问题,跟长度,面积相关的我们完全可以采用这种方式来解题,但需要注意的是,尺子为普通尺子就好,简单点的就好。上面不要有太多标记,否则会有作弊嫌疑。
熟能生巧是王道,多刷题把做题速度提上来。预祝大家在考试中取得满意的成绩!









